둘 다 동일한 목적을 가지고 있기 때문에
스피어만 상관 계수, 켄달 타우 계수는 동시에 같이 해보려 한다.
피어슨 상관 계수처럼 두 변수 간 상관 관계를 나타내는 수치지만, 조금 다르다.
피어슨 상관 계수는 변수를 연속형으로 취급하기 때문에 선형 관계를 의미하지만,
얘네들은 변수를 순서형으로 취급하기 때문에 거기서 오는 차이가 조금 있다.
우선 가정에서부터 차이가 있다.
1. 두 변수는 적어도 순서형 변수이다.
2. 두 변수는 단조 관계를 가진다.
여기서 말하는 단조 관계라는 것은 산점도를 그렸을 때,
계속 감소하거나 계속 증가하는 형태를 의미한다.
또한, 변수를 순서형으로 취급하기 때문에 이상치에 덜 민감하다.
가설은 피어슨 상관 계수와 동일하다.
- 귀무 가설 : 상관 계수는 0이다.
- 대립 가설 : 상관 계수는 0이 아니다.
+ 스피어만과 켄달 타우는 목적이 비슷한데,
소표본이면서 동점이 많을 때는 켄달 타우 계수를 더 선호한다고 한다.
# 데이터 불러오기
sample = read.csv("F:/Sw-tastics/Statistics Analysis/example/13. correlation analysis.csv", header = T)
# 산점도
pairs(sample)
# Spearman
library(psych)
spearman = corr.test(sample,
use = 'complete',
method = 'spearman',
adjust = 'none')
spearman$r
spearman$p
# Kendall tau
kendall = corr.test(sample,
use = 'complete',
method = 'kendall',
adjust = 'none')
kendall$r
kendall$phttps://sw-tatistics.tistory.com/40
[R] Pearson correlation coefficient, 피어슨 상관 계수
피어슨 상관 계수는 두 변수의 선형 상관 관계를 계량화한 수치이다. 결과값은 -1~1 사이의 값을 가지고, 1에 가까울수록 양의 상관 관계를 의미하고, -1에 가까울수록 음의 상관 관계를 의미한다.
sw-tatistics.tistory.com
데이터는 이전 포스팅과 동일하게 사용했다.
가정은 위의 글을 참고하고, 결과만 보도록 하자.
# Spearman
library(psych)
spearman = corr.test(sample,
use = 'complete',
method = 'spearman',
adjust = 'none')
spearman$r
spearman$p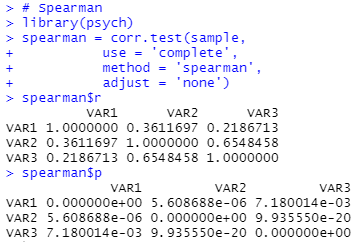
# Kendall tau
kendall = corr.test(sample,
use = 'complete',
method = 'kendall',
adjust = 'none')
kendall$r
kendall$p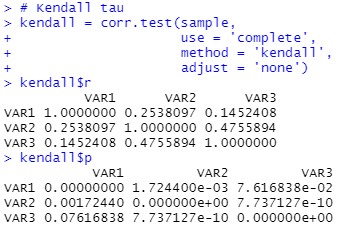
피어슨 상관 계수와 마찬가지로 모든 변수에서 유의한 상관 관계를 확인할 수 있다.
'Statistical Analysis > R' 카테고리의 다른 글
| [R] Linear Regression, 선형 회귀분석(2) - 변수 선택법 (0) | 2022.08.21 |
|---|---|
| [R] Linear Regression, 선형 회귀분석(1) (0) | 2022.07.24 |
| [R] Pearson correlation coefficient, 피어슨 상관 계수 (0) | 2022.07.11 |
| [R] exact McNemar test, 정확 맥니마 검정 (0) | 2022.07.09 |
| [R] McNemar test, 맥니마 검정 (0) | 2022.07.08 |



