[R] Linear Regression, 선형 회귀분석(4) - 고차항/상호작용항

https://sw-tatistics.tistory.com/47?category=1054291 

[R] Linear Regression, 선형 회귀분석(3) - 변수 변환

이전 포스팅에서 종속 변수를 log변환하여 모형을 만들었다.

그 결과, 잔차 그래프는 조금 더 만족스러웠지만, 성능이 감소했다.

이번엔 떨어진 성능을 올려보도록 하자.

 

모형의 성능을 향상시키기 위해선 의미있는 변수를 추가해주면 된다.

새로운 의미있는 변수를 찾는 것도 방법이지만, 기존 변수들을 조작해서 추가하는 것도 도움이 된다.

가장 쉽게 해볼만한 것이 고차항과 상호작용항을 넣는 것이라 생각된다.

 

고차항을 넣으면 어떻게 될까?

모형이 커브 형태의 변화에 대해 설명력을 더 가질 수 있게 된다.

X와 Y 2차원 산점도를 그렸을 때, 커브 형태로 변화하고 있다면 고차항이 모형 성능에 도움이 될 것이다.

 

상호작용항을 넣으면 어떻게 될까?

위와 비슷하지만, 조금 더 직관적인 이해는 어렵긴 하다.

X1, X2와 Y의 3차원 산점도를 그렸다고 치자.

X1과 X2가 증가하면서 Y도 함께 증가하는데, X1과 X2가 함께 증가할수록 Y가 더 많이 증가하는 형태라면 도움이 된다.

아마 그림으로 그려보면 입체적인 커브..? 구..?

그런 느낌의 산점도로 그려질 것 같다.

 

설명은 여기까지하고 결과를 보자.

---

# 데이터 불러오기
sample = read.csv("F:/Sw-tastics/Statistics Analysis/example/14. linear regression.csv", header = T)

# 산점도
pairs(sample)

# regression
model = lm(sales ~ ., data = sample)
par(mfrow = c(2, 2))
plot(model)

summary(model)

# selection
model_selection = step(model, direction = 'both',
                       scope = list(lower = ~1))

summary(model_selection)
plot(model_selection)



# log-scale
model_log = lm(log(sales) ~ youtube + facebook, data = sample)
summary(model_log)
plot(model_log)


# polynomial
model_poly = lm(log(sales) ~
                  I(youtube^2) + I(facebook^2) +
                  youtube + facebook +
                  youtube*facebook, data = sample)
summary(model_poly)

model_fin = lm(log(sales) ~
                 I(youtube^2) +
                 youtube + facebook +
                 youtube*facebook, data = sample)
summary(model_fin)
plot(model_fin)

이번 포스팅에서 최종 모형 선택하고 마무리하겠다.

R 문법을 이용하면 더 간단하게 할수도 있는데...

여기서는 몇 개 안 되서 그냥 다 써봤다.

마찬가지로 newpaper 변수는 그냥 바로 제거해버렸다.

먼저, 다 넣은 모형이다.

R^2가 0.9가까이 증가했다.

근데 facebook의 이차항이 거슬리니까 제거해보자.

 

R^2가 조금 감소했지만, 이 정도면 괜찮아보인다.

 

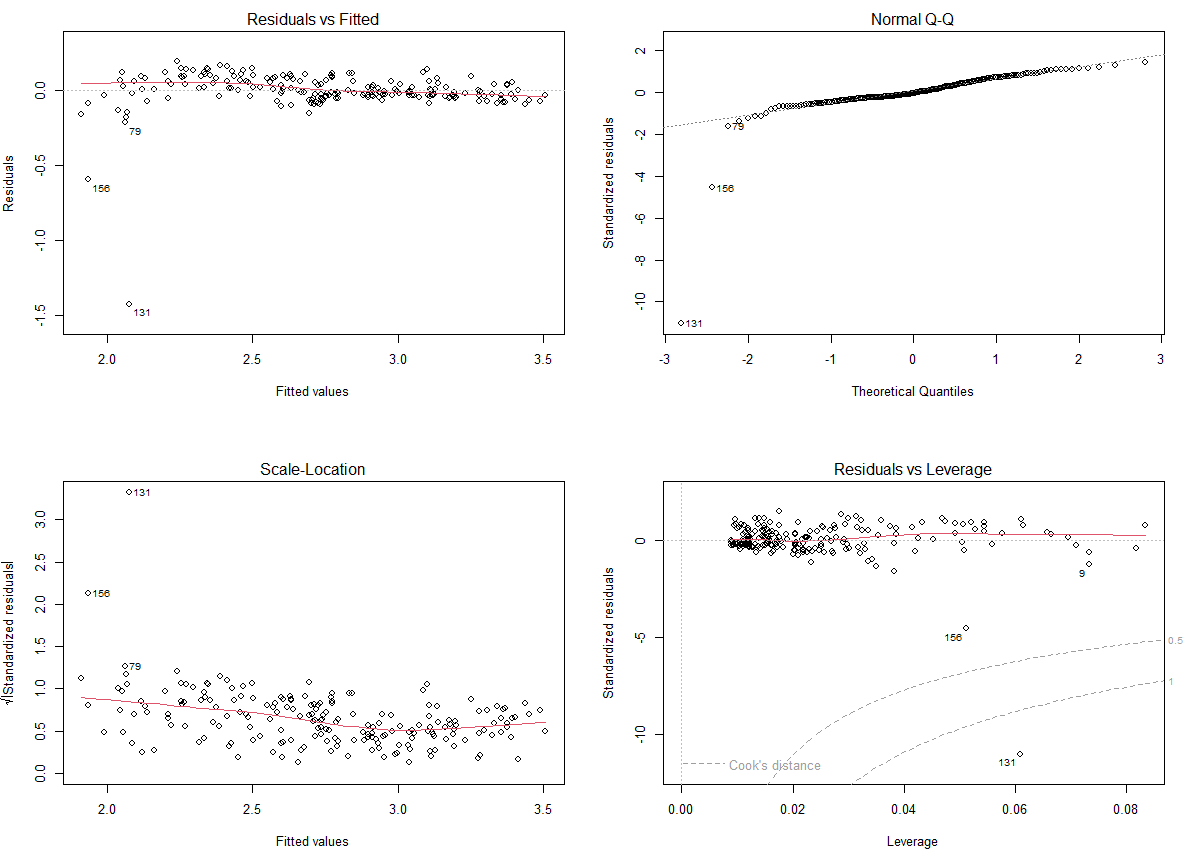
잔차 그래프도 처음에 비해 꽤 괜찮아진 것 같다.

131번 관측치는 계속 거슬리긴 하지만, 위를 최종 모형으로 마무리하려한다.

복잡한 도메인임에도 변수가 별로 없기 때문에 더 해볼만한 게 떠오르지 않기 때문...

 

포스팅의 앞 부분에서 의미있는 변수를 추가하면 성능이 올라간다고 했다.

새로운 변수를 추가하는 것 뿐만 아니라 기존 변수를 이용해서도 이렇게 성능을 올릴수도 있었다.

의미 없었던 변수들로 의미 있는 변수를 만들수도 있고,

의미 있는 변수들로 또 다른 의미있는 변수를 만들수도 있다.

물론, 반대도 되겠지만..

 

어쨌든 주의해야할 점은 무작정 성능에만 몰입하지 않는 것이다.

단순하게 R^2 또는 빈약한 Test Case에 대한 측정 결과만을 이용해 성능을 올리게 된다면 과적합의 위험이 있다.