Paired Sample t-test, 대응 표본 T 검정은
동일한 대상에게서 얻은 "값 차이"의 평균을 비교하는 검정법이다.
쉽게 생각하면 전/후 비교라고 보면 된다.
다이어트 프로그램 전/후 몸무게 비교 같은..
미리 이야기하자면,
대응표본 T검정과 일 표본 T검정과 동일하다고 보면된다.
비교할 값의 차이를 일표본 T검정한다고 생각하면 좋다.
그렇기 때문에 분석의 가정도 정규성 가정만 존재한다.
약간의 차이가 있다면,
비교할 값의 차이가 정규성을 가진다는 것이다.
가설도 거의 비슷하다.
- 귀무 가설 : 비교할 값의 차이의 평균은 0이다.
- 대립 가설 : 비교할 값의 차이의 평균은 0이 아니다.
대입하듯이 문장을 만들고보니 조금 어색한데,
쉽게 생각하면 값의 차이가 없다/있다 정도로 보아도 될듯하다.
# 데이터 불러오기
sample = read.csv("F:/Sw-tastics/Statistics Analysis/example/03. Paired sample t-test.csv", header = T)
# 정규성 검정(shapiro-wilks test)
shapiro.test(sample$before - sample$after)
# t-test
t.test(sample$after,
sample$before,
paired = TRUE)
위는 대응 표본 T검정의 코드이다.
코드 결과를 확인하고, 일표본 T검정을 사용하는 방법도 알아보자.
# 데이터 불러오기
sample = read.csv("F:/Sw-tastics/Statistics Analysis/example/03. Paired sample t-test.csv", header = T)
데이터는 위와 같은 형태이고, 20개의 관측치를 가진다.
# 정규성 검정(shapiro-wilks test)
shapiro.test(sample$before - sample$after)
두 값의 차이에 대한 정규성 검정을 실시한다.
p-value가 0.05보다 크므로 정규성이 만족한다고 하자.
# t-test
t.test(sample$after,
sample$before,
paired = TRUE)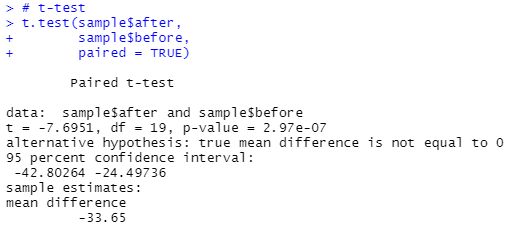
가정을 만족하니, T검정을 실시한다.
p-value가 0.05보다 작으므로 귀무가설을 기각하고,
before과 after의 차이가 있다고 할 수 있다.
# 값의 차이 구하기
sample["diff"] = sample$after - sample$before
# 정규성 검정(shapiro-wilks test)
shapiro.test(sample$diff)
# t-test
t.test(sample$diff)이렇게 값의 차이를 구해서 일표본 T검정으로 확인할 수도 있다.
결과는 동일하니 궁금하다면 해보도록 하자.
'Statistical Analysis > R' 카테고리의 다른 글
| [R] Wilcoxon rank sum test, 윌콕슨 순위합 검정 (0) | 2022.06.21 |
|---|---|
| [R] Wilcoxon signed rank test, 윌콕슨 부호 순위 검정 (0) | 2022.06.21 |
| [R] Independent Sample t-test, 독립 표본 t 검정 (0) | 2022.06.19 |
| [R] One Sample t-test, 일 표본 t 검정 (0) | 2022.05.14 |
| R studio for Windows 설치 (0) | 2022.04.25 |



