윌곡슨 부호 순위 검정은
일표본/대응표본 T검정에 대응되는 비모수 검정법이다.
비모수 검정법에 대해 간단하게 언급해보자면..
앞서 정리한 T검정 내용 중에 "가정"이라는 것이 있었다.
말 그대로 검정법을 수행하기 위한 전제 정도로 생각하면 되는데,
이 가정이 성립하지 않는다면??
예컨데, 정규성 가정이 성립되지 않는 경우가 있겠다.
이처럼 가정을 충족할 때, 시행하는 검정법을 모수 검정법이라고 보면 되고,
가정이 충족되지 않을 때, 사용하는 것이 비모수 검정법이라고 보면 된다.
일반적으로는 모수 검정법의 검정력이 더 뛰어나다.
그렇기 때문에 가능하면 모수 검정법을 시행하는 것이 유리하다고 볼 수 있다.
다시 돌아와서,
"일표본/대응표본 T검정에서 정규성 가정이 만족되지 않을 때"
윌콕슨 부호 순위 검정을 사용하면 된다.
모수 검정법의 가정이 충족되지 않을 때 사용한다고 해서
비모수 검정법의 가정이 없는 것은 아니다.
윌콕슨 부호 순위 검정의 가정은 다음과 같다.
1. 표본은 동일한 모집단에서 추출되어야 한다.
2. 표본은 임의 , 독립적으로 추출되어야 한다.
3. 측정값은 최소 등간척도이다.
가정이 있긴하지만, 상당히 완화된 가정임을 확인할 수 있다.
가설에서도 조금의 변화를 갖는다.
T검정이 평균을 비교하는 것이었다면
윌콕슨 부호 순위 검정은 중앙값을 비교하는 것이다.
따라서, 가설은 다음과 같다.
- 귀무가설 : 모집단의 중앙값은 M이다.
- 대립가설 : 모집단의 중앙값은 M이 아니다.
# 데이터 불러오기
sample = read.csv("F:/Sw-tastics/Statistics Analysis/example/04. Wilcoxon signed rank test(one-sample).csv", header = T)
# 정규성 검정(shapiro-wilks test)
# 일반적으로 관측치가 10개 미만일 때는 정규성을 만족하지 않는다고 한다.
# wilcoxon signed rank test
wilcox.test(sample$weight, mu = 100)일표본의 예시를 먼저 보자.
# 데이터 불러오기
sample = read.csv("F:/Sw-tastics/Statistics Analysis/example/04. Wilcoxon signed rank test(one-sample).csv", header = T)
총 9개의 관측치로 이루어진 데이터이다.
관측치가 적을 경우에는 정규성 검정을 하지 않고도 만족하지 않는다고 한다.
(보통 10개 미만을 기준으로 잡는다.)
따라서, T검정을 시행하기에는 정규성 가정이 충족되지 못 하고,
비모수 검정인 윌콕슨 부호 순위 검정으로 눈을 돌려야한다.
윌콕슨 부호 순위 검정의 가정을 살펴보자.
(1), (2) 가정은 표본 추출에서 문제가 없다면 충족할 것이고,
현재 변수가 무게이기 때문에 가정 (3)도 만족하게 된다.
# wilcoxon signed rank test
wilcox.test(sample$weight, mu = 100)
무게의 중앙값이 100인지/아닌지에 대한 가설을 세우고 검정을 돌려보자.
p-value가 0.05보다 크므로 귀무가설을 기각할 수 없다.
따라서, 무게의 중앙값이 100이 아니라고 할 수 없다.
# 데이터 불러오기
sample = read.csv("F:/Sw-tastics/Statistics Analysis/example/05. Wilcoxon signed rank test(paired-sample).csv", header = T)
# 정규성 검정(shapiro-wilks test)
# 일반적으로 관측치가 10개 미만일 때는 정규성을 만족하지 않는다고 한다.
# wilcoxon signed rank test
wilcox.test(sample$before,
sample$after,
paired = T)이번엔 대응표본 예시이다.
# 데이터 불러오기
sample = read.csv("F:/Sw-tastics/Statistics Analysis/example/05. Wilcoxon signed rank test(paired-sample).csv", header = T)
데이터의 형태는 위와 같다.
관측치는 총 8개이므로 정규성 가정을 만족하기 어렵다고 판단.
비모수 검정으로 결정한다.
가정은 위와 같은 이유로 충족한다고 하자.
# wilcoxon signed rank test
wilcox.test(sample$before,
sample$after,
paired = T)
p-value가 0.05보다 작으므로 귀무가설을 기각하고,
전/후 중앙값은 다르다고 볼 수 있다.
# 값의 차이 구하기
sample["diff"] = sample$after - sample$before
# wilcoxon signed rank test
wilcox.test(sample$diff)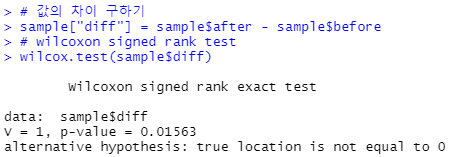
대응표본 T검정에서 확인한 것처럼
여기서도 대응표본->일표본으로 바꾸어 시행할 수 있다.
'Statistical Analysis > R' 카테고리의 다른 글
| [R] Analysis of Variance(ANOVA), 분산 분석 (0) | 2022.06.23 |
|---|---|
| [R] Wilcoxon rank sum test, 윌콕슨 순위합 검정 (0) | 2022.06.21 |
| [R] Paired Sample t-test, 대응 표본 t 검정 (0) | 2022.06.19 |
| [R] Independent Sample t-test, 독립 표본 t 검정 (0) | 2022.06.19 |
| [R] One Sample t-test, 일 표본 t 검정 (0) | 2022.05.14 |



