https://sw-tatistics.tistory.com/42
[R] Linear Regression, 선형 회귀분석(1)
선형 회귀분석은, 독립 변수와 종속 변수 간 관계를 수리적 함수로 만드는 것이다. 함수로 만드는 목적은 단순 명료하다. 함수로 표현함으로써 독립 변수를 이용해 종속 변수를 예측할 수 있고,
sw-tatistics.tistory.com
이전 포스팅에서 간단한 회귀 모형을 만들어 보았다.
해당 모형도 통계적 가정이 조금 아쉬울 뿐이지 성능적으로는 나쁘지 않다고 볼수도 있지만...
그래도 개선시킬 여지가 있어보이니 조금만 더 해보자.
모형을 개선시키는 방법에는 여러가지가 있겠지만,
불필요한 독립 변수를 제거하는 것도 하나의 방법이다.
불필요한 변수가 들어간다면, 쓸데없이 모형이 복잡해질 뿐더러 잘못된 모형이 나올지도 모른다.
변수를 선택하는 통계적인 접근법이 있는데,
보통 AIC나 BIC같은 것을 기준으로 선택을 하게 된다.
변수를 모형에 추가/제거함으로써 가장 좋은 모형을 찾는 것인데,
여기서 변수를 추가/제거하는 방법에 따라 크게 3가지 방법이 있다.
1) 전진 선택법 : 가장 좋은 변수를 추가
2) 후진 제거법 : 가장 불필요한 변수를 제거
3) 단계적 선택법 : 추가,제거를 반복하며 최적 변수 탐색
보통은 단계적 선택법을 많이 사용한다.
여기서도 단계적 선택법을 통해 변수를 선택해보자.
# 데이터 불러오기
sample = read.csv("F:/Sw-tastics/Statistics Analysis/example/14. linear regression.csv", header = T)
# 산점도
pairs(sample)
# regression
model = lm(sales ~ ., data = sample)
par(mfrow = c(2, 2))
plot(model)
summary(model)
# selection
model_selection = step(model, direction = 'both',
scope = list(lower = ~1))
summary(model_selection)
plot(model_selection)서론이 길었지만, 코드로는 한줄이면 끝이 난다.
# selection
model_selection = step(model, direction = 'both',
scope = list(lower = ~1))
summary(model_selection)
plot(model_selection)direction이 위에서 말했던 3가지 선택법 중 하나를 선택하는 것이고,
scope를 통해 변수 선택을 할 범위를 정할 수 있다.
lower와 upper를 각각 지정해줄 수 있는데, 위처럼 하면 모든 변수를 체크하게 된다.
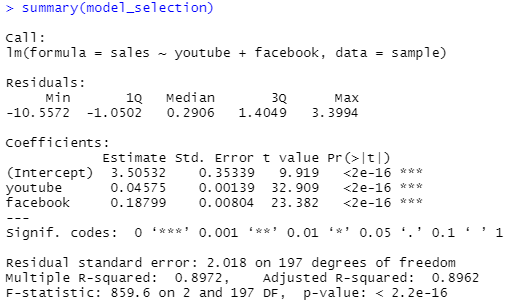
이전 모델과 비교하면, Newspapaer 변수가 제거 되었다.
또한, R^2는 동일하고, adjusted R^2는 오히려 조금 올랐다.
기존 모형에서 Newspaper 변수가 유의하지 않았던 것을 감안하면 제거되는 것이 당연하긴 하다.
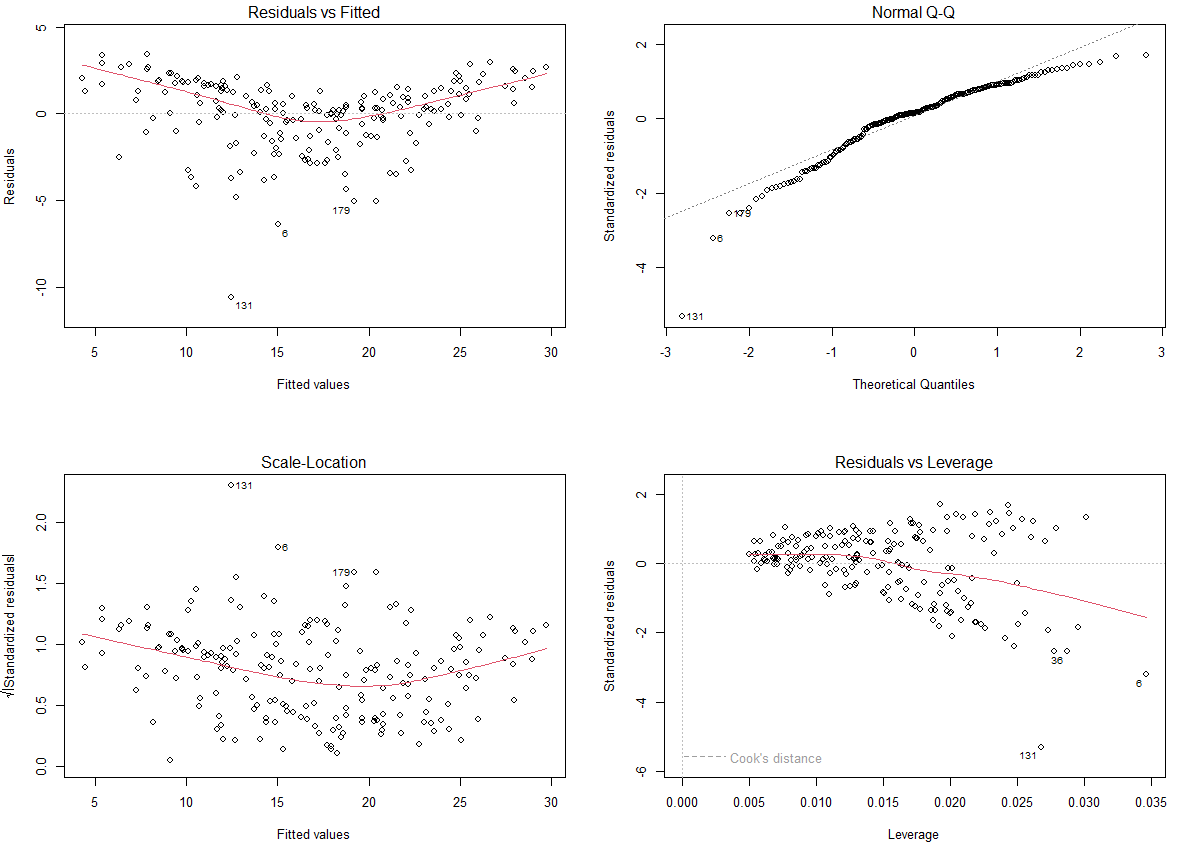
잔차 그래프에서는 큰 차이가 없어보인다.
여전히 조금 아쉬운 느낌이다.
어쨌든 Newspaper 변수는 불필요한 변수라고 판단되어 모형에서는 제거하고,
다음 단계로 가보자.
'Statistical Analysis > R' 카테고리의 다른 글
| [R] Linear Regression, 선형 회귀분석(4) - 고차항/상호작용항 (0) | 2022.08.22 |
|---|---|
| [R] Linear Regression, 선형 회귀분석(3) - 변수 변환 (0) | 2022.08.22 |
| [R] Linear Regression, 선형 회귀분석(1) (0) | 2022.07.24 |
| [R] Spearman correlation coefficient(스피어만 상관 계수), Kendall Tau coefficient(켄달 타우 계수) (0) | 2022.07.12 |
| [R] Pearson correlation coefficient, 피어슨 상관 계수 (0) | 2022.07.11 |



